Regression in Decision Tree — A Step by Step CART (Classification And Regression Tree)
Decision Tree Algorithms — Part 3

1. Introduction
In previous learning has been explained about The Basics of Decision Trees and A Step by Step Classification in CART, This section will explain A Step by Step Regression in CART.
As has been explained, Decision Trees is the non-parametric supervised learning approach. In addition to classification with continuous data on the target, we also often find cases with discrete data on the target called regression. In the regression, the simple way can be to use Linear Regression to solve this case. This time the way to solve the regression case will use a decision tree.
For regression trees, two common impurity measures are:
- Least squares. This method is similar to minimizing least squares in a linear model. Splits are chosen to minimize the residual sum of squares between the observation and the mean in each node.
- Least absolute deviations. This method minimizes the mean absolute deviation from the median within a node. The advantage of this over least squares is that it is not as sensitive to outliers and provides a more robust model. The disadvantage is in insensitivity when dealing with data sets containing a large proportion of zeros [1].
Note : mostly people implement regression case with scikit-learn library, Based on documentation, scikit-learn uses an optimised version of the CART algorithm
2. How Does CART Work in Regression with one predictor?
CART in classification cases uses Gini Impurity in the process of splitting the dataset into a decision tree. On the other hand CART in regression cases uses least squares, intuitively splits are chosen to minimize the residual sum of squares between the observation and the mean in each node. Mathematically, we can write residual as follow

Mathematically, we can write RSS (residual sum of squares) as follow

In order to find out the “best” split, we must minimize the RSS
2.1 Intuition
This simulation uses a “dummy” dataset as follow

The decision tree as follow

2.2 How does CART process the splitting of the dataset (predictor =1)
As mentioned before, In order to find out the “best” split, we must minimize the RSS. first, we calculate RSS by split into two regions, start with index 0
Start within index 0

The data already split into two regions, we add up the squared residual for every index data. furthermore we calculate RSS each node using equation 2.0

Start within index 1
calculate RSS by split into two regions within index 1
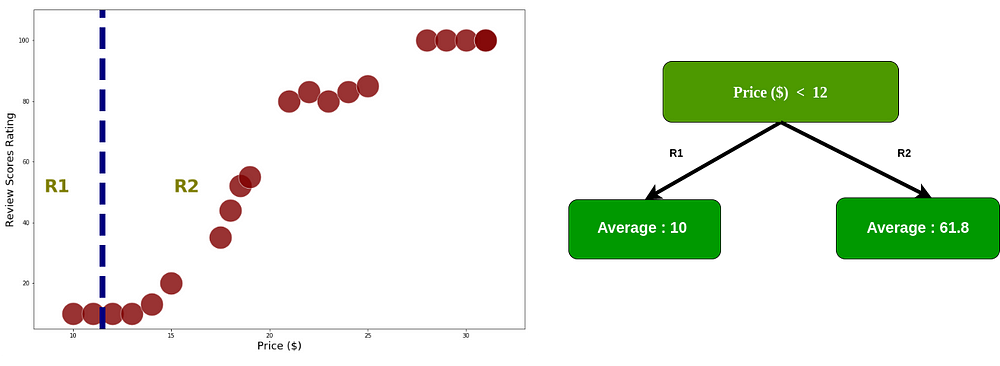
after the data is divided into two regions then calculate RSS each node using equation 2.0

Start within index 2
calculate RSS by split into two regions within index 2

calculate RSS each node

This process continues until the calculation of RSS in the last index
Last Index

Price with threshold 19 has a smallest RSS, in R1 there are 10 data within price < 19, so we’ll split the data in R1. In order to avoid overfitting, we define the minimum data for each region >= 6. If the region has less than 6 data, the split process in that region stops.
Split the data with threshold 19

calculate RSS in R1, the process in this section is the same as the previous process, only done for R1

Do the same thing on the right branch, so the end result of a tree in this case is

2.3 How does CART process the splitting of the dataset (predictor > 1)
This simulation uses a dummy data as following

Find out the minimum RSS each predictor
Price with RSS = 3873.79

Cleaning fee with RSS = 64214.8
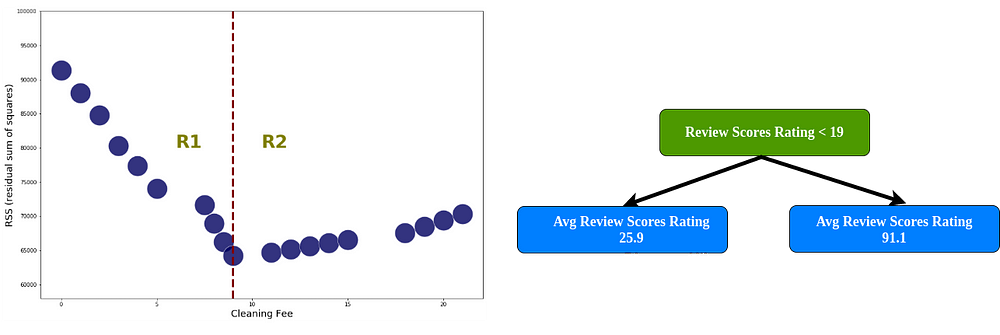
There is only one threshold in License, 1 or 0. So we use that threshold to calculate RSS. License with RSS = 11658.5

We already have RSS every predictor, compare RSS for each predictor, and find the lowest RSS value. If we analyze, License has the lowest value so it becomes root.
The next step can follow the intuition of the Classification in Decision Tree, in the case of classification calculates Gini Impurity, while in the case of regression calculates the minimum RSS. So this is a challenge for you if want to calculate RSS to the end :)
About Me
I’m a Data Scientist, Focus on Machine Learning and Deep Learning. You can reach me from Medium and Linkedin
My Website : https://komuternak.com/
Reference
- Introduction to Statistical Learning
- Ecological Informatics — Classification and Regression Trees
- Adapted from YouTube Channel of “StatQuest with Josh Stamer”
